Automated Objective Method for Assessing Tinnitus Condition
(using fMRI data)
Slides best viewed using Chrome browser. Use ↓|↑|→|← to navigate. First go ↓ all the way, then go →.
www.acnlab.comBackground Information
Functional magnetic resonance imaging is expensive.
A typical machine: $1-3m!
A single scan: $0.5-3k!
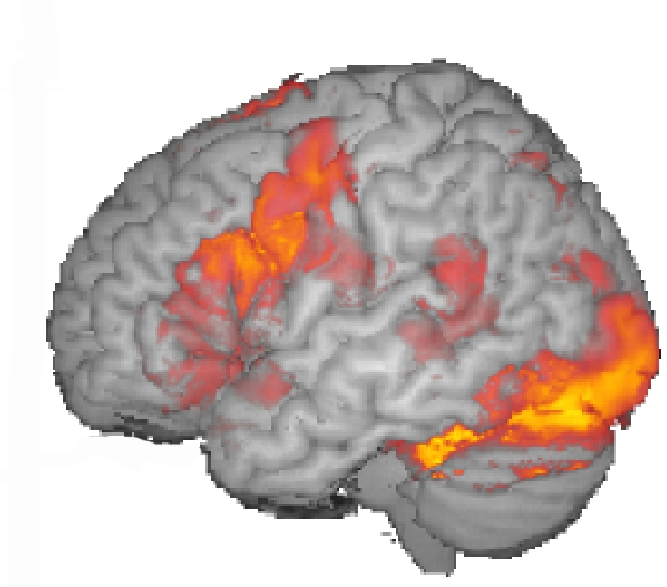
fMRI usually generates multi-dimensional data
Example: fMRI signals from each region of interest in the brain
How to automatically extract meaningful information?
How can we apply machine learning technqiues?
Relatively few approaches amenable to machine learning because:
- Expensive to generate data
- Machine learning needs massive amounts of data
→ Need meaningful dimension reduction methods
Cyclicity analysis
A method to recover ordering and grouping from a set of observed waveforms
We applied the cyclicity method to fMRI data from tinnitus patients
We found that the method can consistently 'fingerprint' a subject
Scans were made in 2 sessions 1 week apart on 47 subjects
Each subject was scanned twice in a session
Scans could be identified as belonging to the same subject using lead matrices from cyclicity analysis!
Lead matrix is a feature generated by cyclicity method
On the grid on the right, each row and corresponding column is assigned to a subject.
Everytime a subject in a row is identified with the subject in a column, that square gets a 1.
Because there were only four scans for each subject, the maximum possible value of a square is 4.
We used a nearest neighbour classifier for identification.
A matrix with a completely yellow diagonal would be perfect!
We could also characterize differences in temporal activation patterns between pairs of brain regions in the control group vs. tinnitus group
This can be visualized using a layered graph
Each node corresponds to a brain region. Brain activity in nodes of the upper layers precedes activity in nodes of the lower layers.
Here, thicker lines correspond to more consistent directional relationship across subjects. A very thin line means that the direction of flow of activity is just as likely to be the opposite.
Left panel is for tinnitus group and the right for the controls. Behaviour of the amygdala is conspicously different in the tinnitus population - replicating findings from other studies.
How does it work?
Big picture:
Cyclicity analysis aims to recover ordering and grouping from a collection of observed waveforms
What does that mean?
Ordering
Say we recorded some waveforms, each of which was delayed from others in phase; a chain of offsets.
Ordering
- Can we say which wave or signal preceded another?
- For example 5 came before 6, which came before 7 and so on.
Grouping
- Can we recover the existence of groups?
- There was a black group and a red group.
Can we still do it if the number of waveforms is very large?
Can we still do it if the waveforms are noisy?
No one wants to inspect that manually ...
... can we automate this recovery?
Yes: Cyclicity analysis allows us to automatically recover this information from large data sets.
Key idea: What is 'cyclic'?
Remark: The following is slightly technical. You can skip ahead if you prefer to see examples.
Key idea: What is 'cyclic'?
Recall, a periodic signal $f(t)$ repeats itself with a consistent period $P$.
\[ f \left( t + P \right) = f \left( t \right) \]A cyclic signal repeats itself inconsistently, i.e. $P$ can vary.
Cyclic signal
Cyclic signals generalize periodic signals.
More precisely, $g(t)$ is cyclic if a monotonically increasing bounded function $\phi(t)$ can be found so that $g \left( \phi (t) \right)$ is periodic.
All periodic signals are cyclic; converse is not true.
Information recovery
Consider two waveforms with the same starting and ending points that are shifted a little in time.
In the figure clearly the wave $Y$ preceded the wave $X$.
Plotted against each other they enclose an area; in-fact a signed area.
The area is signed because it can be positive or negative.
The sign depends on how the closed loop is traversed as the area is calculated.
By convention, we assume clockwise traversal; and if the area is positive, $Y$ follows $X$.
Given $n$ waveforms, cyclicity method analyzes all $n \choose 2$ possible areas at once to recover ordering and grouping.
Example 1
Periodic signals
Consider 12 sinusoids with phase offsets $v_k$ chosen at random.
CTRL/ALT + Click to zoom!
They have been grouped into sets (red, blue, etc.) and numbered according to first appearence
Note that two of the signals also have different magnitudes compared to the rest of the waves
Cyclicity analyzes 66 signed areas to approximately determine $v_k$ which are complex: $v_k= a_k + i b_k$
We plot $v_k$ on the complex plane.
The ordering and grouping is recovered as well as relative magnitude.
Example 2
Non-periodic signals
The signals need not be periodic ...
... they only have to be cyclic and exhibit the chain of offsets property.
The information is recoverable if a certain matrix associated with the areas is "nearly rank 2".
Ordering is preserved and we can still capture that signals 5-6 and signals 2-3 are close together.
Grouping is now approximate. For example 8 is now closer to 1 than it is to 7.
Example 3
Noisy signals
The signals can be noisy...
... say with a stationary noise distribution.
Here SNR=20 and noise is additive white gaussian.
The offsets are uniformly spaced befween 0 and $\pi$.
The ordering is still recoverable!
Angles measured from the horizontal axis to each point are within $ \left[ -k\pi, k \pi \right]$ for some $k \in \left[0,1 \right]$.
Take away:
Cyclicity analysis is an interpretable feature generation method. It can be useful when one wants to automatically investigate temporal patterns.
On-going work using features generated by cyclicity method shows promise in using supervised machine learning to differentiate tinnitus subjects from controls.
Try demo available here. More features coming!